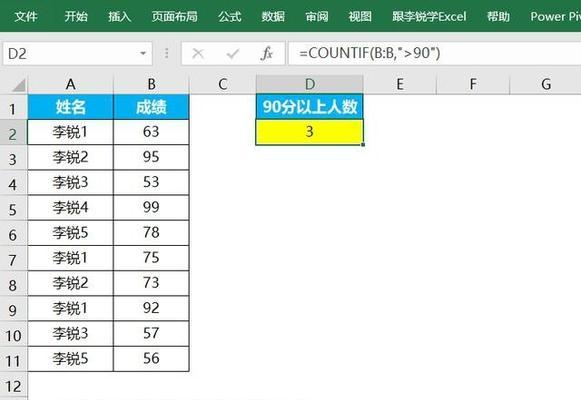
对数函数的定义域及求解方法(探索对数函数的定义域和求解技巧)
游客 2024-08-25 13:52 分类:电子设备 65
对数函数是高中数学中重要的一类函数,其定义域的求解方法也是学习这一概念的关键。本文将讨论对数函数的定义域的概念以及如何求解对数函数的定义域,旨在帮助读者更好地理解和运用对数函数。

一、基础知识:对数函数的概念
1.1对数函数的定义与特点
在数学中,对数函数是指以某个正实数为底的指数函数,记作y=log?(x),其中a>0且a≠1。对数函数有着许多特点,例如对数函数的图像与指数函数图像互为镜像等。
二、定义域概念及求解方法
2.1定义域的概念
在数学中,函数的定义域是指使函数有意义的实数,即输入值的范围。对数函数的定义域也需要满足一定的条件才能使得函数有意义。
2.2对数函数定义域的求解方法
对于常见的对数函数,可以通过一些求解方法来确定其定义域。对于底数为e的自然对数函数ln(x),其定义域为所有正实数;对于底数为10的常用对数函数log??(x),其定义域为正实数。
三、求解对数函数定义域的具体步骤
3.1步骤一:排除分母为零的情况
对于对数函数,由于对数函数在x=0时没有定义,因此在求解定义域时需要排除分母为零的情况。
3.2步骤二:排除负数的情况
对于底数为正实数a的对数函数,其定义域中不包括负数,因此需要排除x<0的情况。
3.3步骤三:排除指数小于等于零的情况
对于底数为正实数a的对数函数,其定义域中指数必须大于零,因此需要排除x≤0的情况。
3.4步骤四:综合考虑多个条件
对于复合形式的对数函数,需要综合考虑多个条件来求解定义域。对于f(x)=log?(g(x)),需要同时满足g(x)>0和x>0才能使得f(x)有意义。
四、实例分析:求解对数函数的定义域
4.1实例一:求解ln(x)的定义域
以自然对数函数ln(x)为例,详细介绍了如何通过定义域求解方法来确定其定义域。根据步骤,可得ln(x)的定义域为x>0。
4.2实例二:求解log??(x+2)的定义域
以常用对数函数log??(x+2)为例,详细介绍了如何应用定义域求解方法来确定其定义域。根据步骤,可得log??(x+2)的定义域为x>-2。
五、小结:掌握对数函数的定义域求解方法
通过本文的学习,我们了解到对数函数的定义域是指使函数有意义的实数,需要满足一定的条件。同时,我们还学习了一些求解对数函数定义域的具体步骤和方法。掌握了这些知识和技巧,我们可以更好地理解和运用对数函数。
通过本文的介绍,我们对对数函数的定义域有了更深入的理解,并学会了如何求解对数函数的定义域。通过掌握这些求解方法,我们可以更好地解决与对数函数相关的问题,提高数学应用能力。同时,我们也要注意在求解过程中遵循正确的步骤和方法,确保结果的准确性。
深入探究对数函数的定义域
对数函数是高中数学中重要的一类函数,其定义域的求解对于理解函数的性质和解题具有重要意义。本文将深入探讨对数函数的定义域求解方法,并说明求解定义域的重要性。
1.对数函数的基本概念
对数函数是以某个确定的底数为基数,将正实数x映射到实数y的函数。对数函数的表达式为y=log?x,其中a为底数。
2.对数函数的性质及图像特征
对数函数具有许多独特的性质,包括定义域为正实数、值域为实数、递增性质以及与指数函数的关系等。其图像呈现出一条光滑的曲线,且过点(1,0)。
3.求解对数函数的定义域方法一:基本求解法
对于大多数简单的对数函数,可以通过分析其底数和指数部分来求解其定义域。具体方法是将底数与指数部分分别进行不等式求解,然后取两者的交集。
4.求解对数函数的定义域方法二:复合函数法
对于复杂的对数函数,可以通过将其表示为复合函数的形式来求解其定义域。具体方法是将对数函数与其他已知函数进行组合,然后求解整个复合函数的定义域。
5.求解对数函数的定义域方法三:利用性质法
对于一些特殊形式的对数函数,可以利用对数函数的性质进行求解。当底数大于1时,对数函数的定义域是正实数;当底数在0和1之间时,定义域为正实数中小于1的数。
6.对数函数定义域求解的重要性
对数函数的定义域求解对于理解和应用函数具有重要意义。它能够帮助我们确定函数的取值范围,解决实际问题中的限制条件,并优化函数的应用。
7.对数函数定义域求解的应用举例
通过具体的例题分析,展示对数函数定义域求解在实际问题中的应用。在生物学中研究生物种群增长过程时,对数函数的定义域求解可以帮助确定适宜的生存条件。
8.对数函数定义域求解在求极限中的应用
在求解函数的极限问题中,对数函数的定义域求解起着至关重要的作用。通过求解函数的定义域,可以确定极限的存在性,并帮助我们更好地理解函数的变化趋势。
9.对数函数定义域求解在解方程中的应用
对数函数的定义域求解在解方程问题中也扮演着重要角色。通过求解对数函数的定义域,我们可以确定方程的合法解范围,从而简化解题过程。
10.对数函数定义域求解的挑战及注意事项
在求解对数函数的定义域时,需要注意底数不能为0或负数,同时需要考虑指数、分式等特殊情况。还需注意处理不等式时不等号方向的变化。
11.对数函数定义域求解与其他函数定义域的对比
对数函数的定义域求解方法与其他函数的定义域求解方法存在一定的差异。通过对比与指数函数、多项式函数等的不同,有助于加深对对数函数定义域求解方法的理解。
12.对数函数定义域求解与实际问题的联系
对数函数定义域求解是理论与实践相结合的过程。通过实际问题中的应用,我们可以更好地理解对数函数的定义域求解方法,并将其运用于实际问题的解决中。
13.对数函数定义域求解的扩展应用
对数函数定义域求解方法也可以应用于其他函数类型的求解,例如指数函数、三角函数等。通过扩展应用,我们可以更全面地理解函数的性质和求解方法。
14.对数函数定义域求解的发展历程
对数函数的定义域求解方法并非一蹴而就,经历了漫长的发展历程。通过回顾对数函数定义域求解方法的演变,可以更好地理解其背后的原理和意义。
15.
本文深入探究了对数函数的定义域求解方法,并说明了求解定义域的重要性。掌握对数函数的定义域求解方法,对于理解函数性质、解决实际问题以及在数学学科中的深入研究都具有重要意义。
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌抄袭侵权/违法违规的内容, 请发送邮件至 3561739510@qq.com 举报,一经查实,本站将立刻删除。!
- 最新文章
- 热门文章
- 热评文章
-
- 小精灵蓝牙耳机连接步骤是什么?连接失败怎么办?
- 小屏手机我只推荐这三款?它们的特色功能是什么?
- 华为nova7Pro的双曲面OLED屏和麒麟985芯片有什么优势?常见问题解答?
- 如何在荣耀50se上开启微信分身功能?遇到问题怎么办?
- 小米11与小米11Pro哪个更值得购买?入手前需要考虑哪些因素?
- iPhone12系列售价是多少?配置有哪些特点?
- 红米Note12系列购买建议?如何选择合适的版本和配置?
- 红米k30与k30i有何不同?购买时应该注意什么?
- OPPOR11全面评测?性能如何?拍照效果怎么样?
- 鸿蒙系统如何升级?3种升级方法详解?
- 荣耀60的曲面屏体验如何?1亿像素和4800mAh电池的续航表现怎么样?
- OPPOReno7系列亮点有哪些?为何成为用户关注焦点?
- 华为P40Pro与P40Pro+区别在哪里?
- vivoX80对比vivoX70Pro:哪个更值得购买?
- iPhone11与iPhoneXsMax哪个性价比更高?购买时应该注意哪些问题?
- 热门tag
- 标签列表